Konsep Fungsi Matematika dan Contohnya

Pada topik sebelum ini kalian telah belajar tentang relasi. Masih ingatkah kalian tentang hal itu? Ya, relasi adalah hubungan antara setiap anggota suatu himpunan dengan anggota himpunan lain. Nah, pada topik kali ini kalian akan belajar tentang “fungsi”. Kata “fungsi” dalam matematika digunakan untuk menyatakan suatu hubungan atau kaitan yang khas antara dua himpunan, sehingga fungsi adalah sesuatu yang khas dari suatu relasi antara dua himpunan. Agar lebih jelas, mari kita perhatikan contoh berikut.

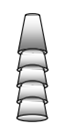
Beberapa gelas dengan tinggi sama (8 cm) disusun seperti pada gambar di atas. Jika gelas kedua dan seterusnya hanya bisa masuk setengah dari tinggi gelas tersebut, maka ukuran tinggi gelas yang tersusun dapat disajikan dalam tabel berikut :

Berdasarkan data di atas, banyak hal yang dapat dipertanyakan, misal :

• “Jika banyak gelas ada 8 buah berapa tinggi tumpukan?”

• “Jika tinggi tumpukan 44 cm, berapa banyak gelas yang disusun?”

• “Jika tinggi sebuah gelas adalah t cm dan banyak gelas ada n, berapa tinggi tumpukan?”

Tinggi tumpukan gelas merupakan “fungsi” dari banyak gelas. Dengan demikian, tinggi tumpukan gelas akan dipengaruhi oleh banyak gelas. Jika tinggi gelas adalah t cm dan banyak gelas adalah n, maka dapat dinyatakan sebuah fungsi yang menghubungkan tinggi gelas dan banyak gelas.

Fungsi ibarat sebuah mesin, ia menerima masukan dan akan menghasilkan keluaran.

Jika dimasukkan informasi mengenai tinggi sebuah gelas dan banyak gelas yang disusun maka akan diperoleh hasil tinggi susunan gelas tersebut. Terlihat bahwa setiap banyak gelas mempunyai pasangan relasi dengan tinggi tumpukan.

Mari kita cermati kasus lainnya.

Misalkan himpunan A = {1, 2, 3} dan B = {a, b, c}, maka beberapa relasi dari himpunan A ke himpunan B yang mungkin adalah :

a) {(1, a), (2, a), (3, a)}

b) {(1, b), (2, b), (3, b)}

c) {(1, b), (2, b), (3, c)}

d) {(1, a), (2, b), (3, c)}

e) {(1, a), (2, b), (2, c)}

f) {(3, a), (2, b), (3, c)}

g) {(1, a), (1, b), (3, c)}

Relasi a), b), c), dan d) merupakan contoh fungsi, sedangkan relasi e), f), dan g) adalah contoh bukan fungsi.

Coba kalian amati, apa bedanya?

Nampak bahwa pada fungsi setiap anggota A mempunyai pasangan dan banyaknya pasangan tunggal, sedangkan relasi yang bukan fungsi ada anggota himpunan A yang tidak punya pasangan atau pasangannya tidak tunggal.

Dengan kata lain, suatu fungsi f dari himpunan A ke himpunan B adalah relasi yang memetakan setiap anggota himpunan A dengan tepat satu pada anggota himpunan B.

Dalam fungsi ini, himpunan A disebut domain (daerah asal), himpunan B disebut kodomain (daerah kawan), dan anggota himpunan B yang memiliki pasangan dengan anggota himpunan A disebut range (daerah hasil).

Jika kita perhatikan fungsi di atas, maka daerah hasilnya adalah

a) {a}

b) {b}

c) {b,c}

d) {a,b,c}

Lalu, bagaimana cara menyatakan fungsi?

Nah, fungsi dapat dinyatakan dalam beberapa bentuk, yaitu :

1. Himpunan pasangan berurutan

Diketahui fungsi f dari A = {1, 2, 3, 4, 5} ke B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} dengan relasi “setengah dari”, maka fungsi f dapat dinyatakan menjadi dalam himpunan pasangan berurutan , yaitu : {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)}

2. Diagram panah

Diketahui fungsi f dari A = {1, 2, 3, 4, 5} ke B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} dengan relasi “setengah dari”, maka fungsi f dapat dinyatakan menjadi dalam diagram panah, yaitu

3. Rumus fungsi

Diketahui fungsi f dari A = {1, 2, 3, 4, 5} ke B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} dengan relasi “setengah dari”, maka diperoleh relasi berikut :

1. 1R2 dimana 2 = 2 x 1
2. 2R4 dimana 4 = 2 x 2
3. 3R6 dimana 6 = 2 x 3
4. 4R8 dimana 8 = 2 x 4
5. 5R10 dimana 10 = 2 x 5

Untuk setiap x ∈ A = {1, 2, 3, 4, 5} maka (x , 2x) merupakan anggota dari fungsi tersebut. Bentuk ini dapat kita tulis f(x) = 2x dengan x ∈ A. Bentuk f(x) = 2x inilah yang disebut rumus fungsi.

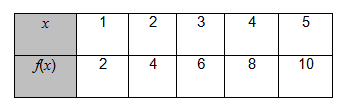
4. Tabel

Fungsi dapat juga dinyatakan dalam tabel. Kita ambil contoh di atas dengan rumus fungsi f(x) = 2x, dapat kita nyatakan dalam tabel berikut :

5. Grafik

Mari kita nyatakan fungsi di atas dengan grafik berikut.

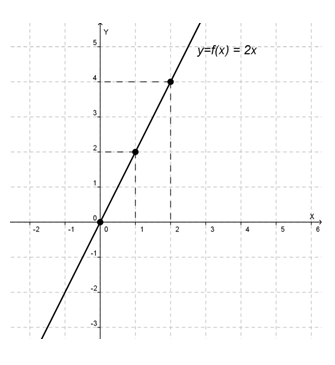
Sudah jelas bukan? Nah, sekarang silakan mencoba soal-soal latihan. Selamat belajar!