Operasi Himpunan dan Contohnya

Pada topik kali ini, kita akan membahas operasi pada himpunan. Sebelum mempelajari materi tersebut, terlebih dahulu kita akan membahas tentang himpunan bagian.

1. Himpunan Bagian

Definisi

Himpunan A merupakan himpunan bagian dari B jika dan hanya jika setiap anggota A juga menjadi anggota B.

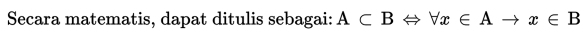
Didefinisikan pula bahwa setiap himpunan kosong merupakan bagian dari himpunan lainnya.

Contoh:

Himpunan bagian dari B = {1, 2} adalah Ø, {1}, {2}, dan {1, 2}.

Tampak bahwa jika n(B) = 2 maka banyak himpunan bagiannya ada 4 = 2^2.

Secara umum dapat dirumuskan bahwa:

Sifat

jika A adalah suatu himpunan dengan n(A) = k maka banyaknya himpunan bagian dari A adalah 2^k

Apakah kalian sudah paham?

Sekarang, mari kita lanjutkan pada pembahasan operasi pada himpunan.

2. Operasi Komplemen

Definisi

Operasi komplemen didefinisikan sebagai berikut.

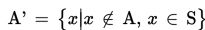
Dibaca “himpunan A’ anggotanya adalah x sedemikian sehingga x bukan anggota A, tapi x anggota S.”

Contoh:

Diketahui S adalah himpunan bilangan asli yang kurang dari 7 dan A = {2, 3, 5}. Coba tentukan A’ dan gambarkan diagram Venn-nya.

Jawab:

S = {1, 2, 3, 4, 5, 6, 7} dan A = {2, 3, 5}

Berdasarkan pengertian operasi komplemen, diperoleh A’ = {1, 4, 6, 7}.

Diagram Venn-nya seperti berikut.

 

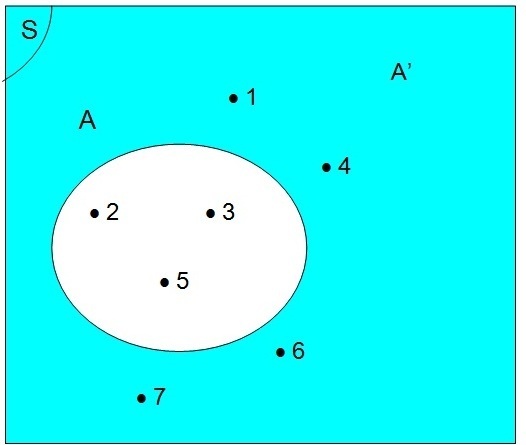
3. Operasi Pengurangan

Definisi

Operasi pengurangan dua buah himpunan dinotasikan dengan “-“, didefinisikan sebagai berikut.

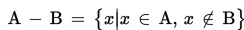
Contoh:

Dari himpunan A = {1, 3, 5, 7} dan B = {2, 4, 6, 8}, diperoleh A – B = {1, 3, 5, 7} = A. Kamu pun dapat mengamati bahwa A dan B adalah himpunan yang saling lepas. Ternyata, untuk himpunan yang saling lepas ini, selisihnya sama dengan himpunan yang dikurangi.